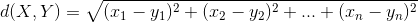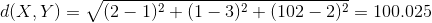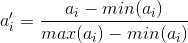| | KNN算法 | K-Means算法 |
| 目标 | 确定某个元素所属的分类 | 将已存在的一系列元素分类 |
| 算法类别 | 监督的分类算法 | 无监督的聚类算法 |
| 数据区别 | 训练数据中,有明确的标签。 如:一个数据集中有几万张图片,都被打上了“苹果”的标签,另外还有几万张图片,被打上了“香蕉”的标签,数据是完全正确,知道结果的数据 | 几十万张各种各样水果的图片放一起,杂乱无章。 |
| 训练过程 | 无需训练(或者没有很明显的训练过程),将数据与训练数据直接对比 | 需要前期训练 |
| K的含义 | K指的是相邻数据的数目。 举个例子,假设某张图片相邻的20张图片中,有18张是打着“苹果”标签的数据,有1张是“香蕉”,1张是“樱桃”,那么这张图片的标签也是“苹果”。 那么在这个例子中,K就是20,20张相邻的图片。 | K指的是分类的数目,人为设定好分为K个簇。 |
| 对比结果 | K值不变的情况下,每次结果都是一样的。 | K值确定后每次结果可能不同。 |
1、KNN算法,本质是一种数据统计的方法。
1.1 欧几里得距离
欧几里得距离通俗来讲就是高中数学中直角坐标系求两点间的距离,二维公式:|x| = √( x2 + y2 )
1.2 距离计算
假设我们现在要对某张图片进行识别,大概是个怎样的思路呢(仅供理解,实际开发中更复杂)?
第一步,将图片黑白化(具体内容很多,这里就不纠结了)。
第二步,用0和1替换黑和白,如下图这就是一个“4”字:

第三步,上图可以看成是一个X行Y列的矩阵,把它变成1行N列的变量,类似于我们直角坐标系中的(X,Y)。
第四步,套用欧几里得度量公式,算出训练数据与当前数据的距离。
第五步,根据设置的K值,获取距离最近的K个变量,取当中出现频率最高的一个标签,假设是标签“4”出现频率最高。
第六步,那么当前数据就属于这个“4”这个标签。判断该图片里面的内容是数字4。
参考源码:https://github.com/NateHuangHao/knn
1.3 劣势
分类作为一种监督学习方法,要求必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别与之对应。但是很多时候上述条件得不到满足,尤其是在处理海量数据的时候,如果通过预处理使得数据满足分类算法的要求,则代价非常大,这时候可以考虑使用聚类算法。
聚类属于无监督学习,相比于分类,聚类不依赖预定义的类和类标号的训练实例。
2、K-Means聚类算法----距离与相异度
在正式讨论聚类前,我们要先弄清楚一个问题:如何定量计算两个可比较元素间的相异度。用通俗的话说,相异度就是两个东西差别有多大,例如人类与章鱼的相异度明显大于人类与黑猩猩的相异度,这是能我们直观感受到的。但是,计算机没有这种直观感受能力,我们必须对相异度在数学上进行定量定义。
2.1 相异度计算
现在有两个变量,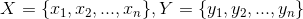 其中X和Y各自具有n个可度量特征属性,那么X和Y的相异度定义为:
其中X和Y各自具有n个可度量特征属性,那么X和Y的相异度定义为: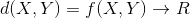 ,其中R为实数域。也就是说相异度是两个元素对实数域的一个映射,所映射的实数定量表示两个元素的相异度。
,其中R为实数域。也就是说相异度是两个元素对实数域的一个映射,所映射的实数定量表示两个元素的相异度。
这里又要提到之前说到的欧几里得距离: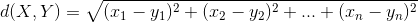
例如,计算 X={2,1,102} 和 Y={1,3,2} 的相异度:
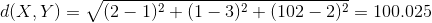
这里存在一个问题,就是取值范围大的属性对距离的影响高于取值范围小的属性
XY两个元素的第三个属性102和2的差值太大了,这样就导致相异度反映不够真实,为了解决这个问题,一般要对属性值进行规格化。
所谓规格化就是将各个属性值按比例映射到相同的取值区间,这样是为了平衡各个属性对距离的影响。通常将各个属性均映射到[0,1]区间,映射公式为:
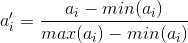
其中max(ai)和min(ai)表示所有元素项中第i个属性的最大值和最小值。例如,将示例中的元素规格化到[0,1]区间后,就变成了X’={1,0,1},Y’={0,1,0},重新计算欧氏距离约为1.732。
2.2 聚类算法
所谓聚类,就是给定一个元素集合D,其中每个元素具有n个可观察属性,使用某种算法将D划分成k个子集,要求每个子集内部的元素之间相异度尽可能低,而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇。
k均值算法的计算过程非常直观:
1、从D中随机取k个元素,作为k个簇的各自的中心。
2、分别计算剩下的元素到k个簇中心的相异度,将这些元素分别划归到相异度最低的簇。
3、根据聚类结果,重新计算k个簇各自的中心,计算方法是取簇中所有元素各自维度的算术平均数。
4、将D中全部元素按照新的中心重新聚类。
5、重复第4步,直到聚类结果不再变化。
6、将结果输出。

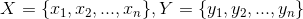 其中X和Y各自具有n个可度量特征属性,那么X和Y的相异度定义为:
其中X和Y各自具有n个可度量特征属性,那么X和Y的相异度定义为: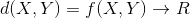 ,其中R为实数域。也就是说相异度是两个元素对实数域的一个映射,所映射的实数定量表示两个元素的相异度。
,其中R为实数域。也就是说相异度是两个元素对实数域的一个映射,所映射的实数定量表示两个元素的相异度。