对于一个整天写增删改查的java程序员,厌倦了成天搬砖,所以最近研究了一下递归.首先声明,本人非科班出身,对于刚接触递归就感觉有一种莫名高大上算法的赶脚,本着好奇+梦想成为牛逼攻城狮的想法,就来探一探递归算法的究竟.

1.递归是什么?

      定义:程序调用自身的编程技巧称为递归--百度词条.

      不明白的,一直可以点该链接:递归.(出口就是右上角x)

      我们平常对于解决同样问题的孪生兄弟:迭代,它使用的是循环结构,而递归使用的则是选择结构.对于这点看不明白不要紧,请先抛开硬生生的概念,思考以下问题,并在脑海里撸着代码(脑补):

首先我们思考一下1+2+3....+100=?要怎么写程序来计算呢?很多人第一反应来使用for循环:

		int sum =0; 		for (int i = 1; i <= 100; i++) { 			sum+=i; 		} 		System.out.println(sum);//5050

或者二逼青年使用最简洁而且高效的公式(推荐使用,开销最小,且一步到位):

		int start =1; 		int end = 100; 		int sum =(start+end)*end/2;//首项加末项乘以项数除以二 		System.out.println(sum);//5050

而递归代码如下:

    static  int  test1(int n){ 		if(n==1){//递归出口 			return 1; 		}else{ 			return n+test1(n-1); 		} 	}

通过初体验对比,不难发现以下递归有以下几个特点:

    1.优点:使程序结构更清晰,更简洁,更容易让人理解,递归要有出口,不然成了死循环.

    2.缺点:使用递归调用时，如果过多的调用容易造成java.lang.StackOverflowError即栈溢出和程序执行过慢。这是一个潜在Bug和影响程序执行效率问题，需要谨慎使用。

对于互联网这种以速度和效率来维护用户量,建议直接找本文章的递归出口.但既然看到了这里,不妨锻炼下自己的思维.

2.递归的执行过程:

    递归函数分为调用和回退阶段,递归的回退顺序是它调用顺序的逆序.说起来比较拗口举个例子就明白了,在此也明显的可以看出,递归是选择结构:

这个不难写出递归的程序:            

    static  int  factorial(int n){ 		if(n==0){ 			return 1; 		}else{ 			return n*factorial(n-1); 		} 	}

它的调用顺序是怎么样的呢

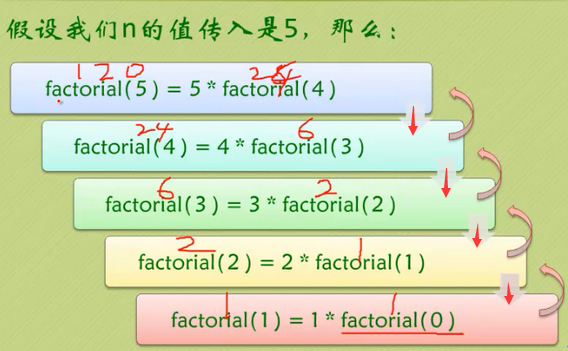
或者这样:

调用

回退

当factorial(0)时,开始回退.

3.递归算法实例讲解

现在,大家最递归是不是有一个感性的认识了,最起码知道简单的用法l了,接下来我们不妨提升一下难度,以下题目请先思考,并不要急着看代码(最好思考递归和迭代两种方式实现),第一道题可能你会经常在面试题里看到,如果知道程序的写法,或者说已经理解,请直接跳到后面的题目. 

1.题目:有一对兔子，从出生后第3个月起每个月都生一对兔子， 小兔子长到第四个月后每个月又生一对兔子， 假如兔子都不死，问每个月的兔子总数为多少?

分析,这个题目是著名的斐波那契数列:1,1,2,3,5,8,13,21....=Sn = Sn-1+Sn-2

规律是:从第三个数开始,每个数都是前两个数的合.

迭代方式:

		    int month =10;  	        int sum[]= new int[month] ; //初始化月份数组 	        sum[0] = 1; //第一个月 	        sum[1] = 1; //第二个月 	              	        for(int i=2;i<=month-1;i++){  	            sum[i] = sum[i-1]+sum[i-2]; //第三个月等于前两个月之和 	        }  	                  	        System.out.println("第"+month+"个月的兔子总数是："+sum[month-1]); 

递归方式:

	   static int  recursion(int i){ 	        if( i == 1  || i == 2 ){ 	            return 1; 	        } 	        else{ 	            return  recursion(i-1) +  recursion(i-2);//第三项等于后两项之和 	        } 	    }

2.题目: 递归逆序排列字符单词,例:I love java--->java love I

迭代的方式就不在演示,重点在递归如何实现:

    static String reverse(String s) { 		int i = s.indexOf(" ");//搜索第一次出现" "的位置 	    if (s == null||i == -1) { 	      return s; 	    } 	    return reverse(s.substring(i + 1)) + " " + s.substring(0, i);//每次截取第一个单词放在最后拼接 	}

3.题目:使用递归来统计字符串String str="hello"的长度,不能使用统计变量.

   static int test1(String str){ 		if(null==str||str.equals("")){ 			return 0; 		} 		String[] strs = str.split(""); 		StringBuffer sb = new StringBuffer();//每次截取最后一个字母 		for(int i = 0; i <= strs.length-2; i++) 		{  		    sb. append(strs[i]); 		} 		return test1(sb.toString())+1;//每次递归调用+1 	}

4.题目:二分查找算法:不断将数组进行对半分割，每次拿中间元素和goal进行比较(前提是数组元素的排序应该是递增或者递减)

    public static void main(String[] args) { 		int [] arr={1,2,5,6,8,9,12,64,78,90};//有序数组 		System.out.println(test(arr,0,arr.length-1,8));//传入数组和数组长度,最后一个是要查找的值 	} 	//递归方式实现 	public static int recursion(int [] arr,int low,int high,int value){ 		if(low>high){ 			return -1; 		} 		int mid=(low+high)/2;//求中间的值 		if(value==arr[mid]){//如果相等,则找到该值,直接返回 			return mid; 		}else if(value<arr[mid]){//如果要找的值在中间值得左边,则下一次递归开始的右指针指向该次中间值-1 			return recursion(arr,low,mid-1,value); 		}else{////如果要找的值在中间值得右边,则下一次递归开始的左指针指向该次中间值+1 			return recursion(arr,mid+1,high,value); 		} 	} 	//迭代方式实现 	public static int test(int [] arr,int low,int high,int value){ 		int mid; 		while(high>=low){ 			mid=(low+high)/2; 			if(value<arr[mid]){ 				high=mid-1; 			}else if(value>arr[mid]){ 				low=mid+1; 			}else{ 				return mid; 			} 		} 		return -1;//都没找到,则返回-1 	}

5.题目:求最大公约数和最小公倍数:

	public static void main(String[] args) { 		int x = 100; 		int y =  18; 		System.out.println("最大公约数:"+gcd(x,y)); 		System.out.println("最小公倍数:"+lcm(x,y)); 	} 	//辗转相除法 	public static int  gcd(int  x,  int y) { 	    if (y == 0){ 	        return x;         }else{ 	        return gcd(y, x % y);//x%y时,如果x<y则返回x,例:4%20=4  5%20=5,迭代之后会把小数放在后面         } 	}   //最小公倍数　       public static int lcm(int p,int q){             int pq = p * q;             return pq / gcd(p,q);        } 

6.题目:杨辉三角

        1 
       1 1 
      1 2 1 
     1 3 3 1 
    1 4 6 4 1 
   1 5 10 10 5 1 
1 6 15 20 15 6 1 

分析:杨辉三角最本质的特征是，它的两条斜边都是由数字1组成的，而其余的数则是等于它肩上的两个数之和。

	public static void main(String[] args) { 		int n = 7; 		for (int i = 1; i <= n; i++) { 			for (int j = 1; j <= n-i; j++) { 				System.out.print(" "); 			} 			for (int j = 1; j <= i; j++) { 				System.out.print(num(i,j)+" "); 			} 			System.out.println(); 		} 	} 	public static int num(int x,int y){ 		if(y==1||y==x){ 			return 1; 		} 			return num(x-1,y-1)+num(x-1,y);//每一个数等于肩上两个数之和 	}

7.题目:汉诺塔

接下来就到了最后的压轴,汉诺塔!本文就不对汉诺塔游戏规则进行讲解.但可以理解一下它的思想,递归和数学中的归纳本质上是相同的,汉诺塔最小移动次数会生成的数列如下:

0,1,3,7,15,63...表达式为:f(n)=2^n  - 1,可以用数学归纳法来证明该解析式的正确性.

连接:证明并推导汉诺塔（河内之塔）问题公式

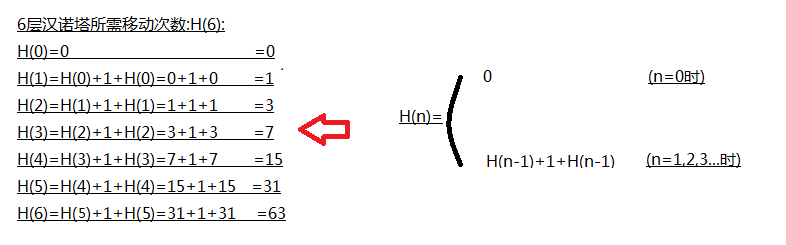
数学功底不够的话,建议先玩玩汉诺塔游戏,总结一下游戏规律,我们这里直接给出程序.

	static int t=0;//最少移动次数 	public static void main(String[] args) { 		hanio(3,"x","y","z"); 		System.out.println(t); 	} 	 static void  hanio(int n ,String src,String mid,String dest){ 		if(n==1){ 			System.out.println(src+"-->"+dest);//移动过程 			t++; 		}else{ 			hanio(n-1,src,dest,mid);//将n-1个盘子借助z移动到y 			hanio(1,src,"",dest);//因为中间柱子没用到,所以可以填""或者填mid,将最大的盘子直接移动到z 			hanio(n-1,mid,src,dest);//将在中间的n-1个盘子借助x移动到z 		} 	}

4.总结和展望

通过本篇文章,可以对递归有个基本的认识:递归用于解决某些特定问题非常方便.实际上,递归和数学中的归纳本质上是相同的.都是"将复杂的问题简化"例如本文最后H(6),6层汉诺塔公式.递归主要思想就是"把握结构",因为把握结构是分解整个问题的突破口.

本文有写的不当之处,还望大家指出.或者有其他解法,欢迎评论区分享交流