上篇描述了HashMap的数据结构原来你是这样的HashMap

本篇就TreeMap的实现进行详述

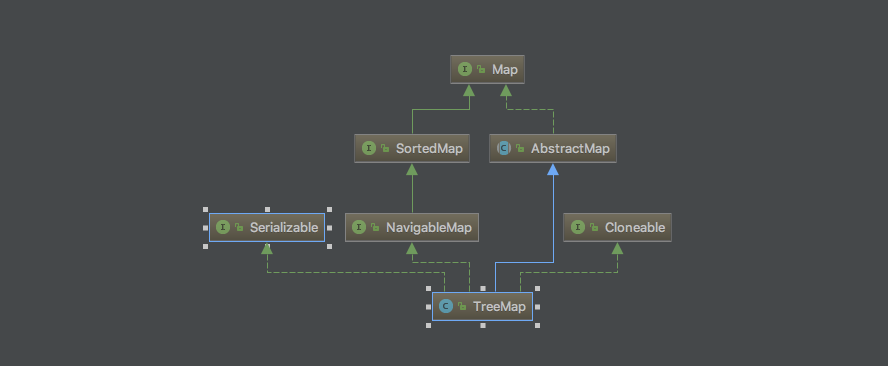
相比较HashMap其多了SortedMap（NavigableMap 类似ceil floor返回最接近的元素）接口实现

顾名思义就是支持了排序

说到排序可能大家就能想到一堆排序算法:堆排序 二分法 冒泡排序 插入排序 快排等等

那么TreeMap采用了红黑树来作为排序（传统的平衡二叉树指的是高度上的平衡一般称之为AVL树，即任意节点的左子树和右子数的高度相差不超过1，红黑树的是平衡指的是黑高度【BH】的的平衡，即任意节点到叶子节点的简单路径中黑色节点数目均相同）

几个常见的构造函数如下

/**  * Constructs a new, empty tree map, using the natural ordering of its  * keys.  All keys inserted into the map must implement the {@link  * Comparable} interface.  Furthermore, all such keys must be  * <em>mutually comparable</em>: {@code k1.compareTo(k2)} must not throw  * a {@code ClassCastException} for any keys {@code k1} and  * {@code k2} in the map.  If the user attempts to put a key into the  * map that violates this constraint (for example, the user attempts to  * put a string key into a map whose keys are integers), the  * {@code put(Object key, Object value)} call will throw a  * {@code ClassCastException}.  */ public TreeMap() {     comparator = null; }   /**  * Constructs a new, empty tree map, ordered according to the given  * comparator.  All keys inserted into the map must be <em>mutually  * comparable</em> by the given comparator: {@code comparator.compare(k1,  * k2)} must not throw a {@code ClassCastException} for any keys  * {@code k1} and {@code k2} in the map.  If the user attempts to put  * a key into the map that violates this constraint, the {@code put(Object  * key, Object value)} call will throw a  * {@code ClassCastException}.  *  * @param comparator the comparator that will be used to order this map.  *        If {@code null}, the {@linkplain Comparable natural  *        ordering} of the keys will be used.  */ public TreeMap(Comparator<? super K> comparator) {     this.comparator = comparator; }   /**  * Constructs a new tree map containing the same mappings as the given  * map, ordered according to the <em>natural ordering</em> of its keys.  * All keys inserted into the new map must implement the {@link  * Comparable} interface.  Furthermore, all such keys must be  * <em>mutually comparable</em>: {@code k1.compareTo(k2)} must not throw  * a {@code ClassCastException} for any keys {@code k1} and  * {@code k2} in the map.  This method runs in n*log(n) time.  *  * @param  m the map whose mappings are to be placed in this map  * @throws ClassCastException if the keys in m are not {@link Comparable},  *         or are not mutually comparable  * @throws NullPointerException if the specified map is null  */ public TreeMap(Map<? extends K, ? extends V> m) {     comparator = null;     putAll(m); }

默认情况下comparator都是空，那么是如何进行排序的呢？

我们查看一下put方法

public V put(K key, V value) {     Entry<K,V> t = root;     if (t == null) {         compare(key, key); // type (and possibly null) check           root = new Entry<>(key, value, null);         size = 1;         modCount++;         return null;     }     int cmp;     Entry<K,V> parent;     // split comparator and comparable paths     Comparator<? super K> cpr = comparator;     if (cpr != null) {         do {             parent = t;             cmp = cpr.compare(key, t.key);             if (cmp < 0)                 t = t.left;             else if (cmp > 0)                 t = t.right;             else                 return t.setValue(value);         } while (t != null);     }     else {         if (key == null)             throw new NullPointerException();         Comparable<? super K> k = (Comparable<? super K>) key;         do {             parent = t;             cmp = k.compareTo(t.key);             if (cmp < 0)                 t = t.left;             else if (cmp > 0)                 t = t.right;             else                 return t.setValue(value);         } while (t != null);     }     Entry<K,V> e = new Entry<>(key, value, parent);     if (cmp < 0)         parent.left = e;     else         parent.right = e;     fixAfterInsertion(e);     size++;     modCount++;     return null; }

看到compare方法

/**  * Compares two keys using the correct comparison method for this TreeMap.  */ final int compare(Object k1, Object k2) {     return comparator==null ? ((Comparable<? super K>)k1).compareTo((K)k2)         : comparator.compare((K)k1, (K)k2); }

看来首先是使用comparator进行排序如果不存在则使用compareTo方法进行排序

那么必然如下问题：

1. TreeMap可否使用key为null
2. TreeMap的key是否Comparable之类
3. 如果comparator发生了变化是否排序会受到影响需要resort？

问题1. 当comparator为空的时候放入空key必然会导致npe发生（和hashMap不一样，有时会用来存空key）

问题2：默认情况下如果放入了不支持排序的类型会导致强转类型失败

问题3：所以TreeMap将comparator设置为final那么该值必然只能设置一次

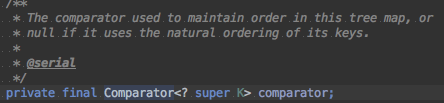
因此在通常场景下TreeMap的key还是需要校验是否为空（和HashMap不一样，当然是用comparator并且comparator支持null的话是OK的）

其实上述描述存在问题，事实上comparator方法不支持compare的参数为空 其详细约定如果为null要抛出npe

/**  * Compares its two arguments for order.  Returns a negative integer,  * zero, or a positive integer as the first argument is less than, equal  * to, or greater than the second.<p>  *  * In the foregoing description, the notation  * <tt>sgn(</tt><i>expression</i><tt>)</tt> designates the mathematical  * <i>signum</i> function, which is defined to return one of <tt>-1</tt>,  * <tt>0</tt>, or <tt>1</tt> according to whether the value of  * <i>expression</i> is negative, zero or positive.<p>  *  * The implementor must ensure that <tt>sgn(compare(x, y)) ==  * -sgn(compare(y, x))</tt> for all <tt>x</tt> and <tt>y</tt>.  (This  * implies that <tt>compare(x, y)</tt> must throw an exception if and only  * if <tt>compare(y, x)</tt> throws an exception.)<p>  *  * The implementor must also ensure that the relation is transitive:  * <tt>((compare(x, y)&gt;0) &amp;&amp; (compare(y, z)&gt;0))</tt> implies  * <tt>compare(x, z)&gt;0</tt>.<p>  *  * Finally, the implementor must ensure that <tt>compare(x, y)==0</tt>  * implies that <tt>sgn(compare(x, z))==sgn(compare(y, z))</tt> for all  * <tt>z</tt>.<p>  *  * It is generally the case, but <i>not</i> strictly required that  * <tt>(compare(x, y)==0) == (x.equals(y))</tt>.  Generally speaking,  * any comparator that violates this condition should clearly indicate  * this fact.  The recommended language is "Note: this comparator  * imposes orderings that are inconsistent with equals."  *  * @param o1 the first object to be compared.  * @param o2 the second object to be compared.  * @return a negative integer, zero, or a positive integer as the  *         first argument is less than, equal to, or greater than the  *         second.  * @throws NullPointerException if an argument is null and this  *         comparator does not permit null arguments  * @throws ClassCastException if the arguments' types prevent them from  *         being compared by this comparator.  */ int compare(T o1, T o2);

理论上都不支持null key

让我们重新来走一遍TreeMap的put过程。

这是一个典型的二叉查找树的查找与插入过程。

1. 如果当树本身不存在的情况下直接将本身放入根并返回空

   Entry<K,V> t = root; if (t == null) {     compare(key, key); // type (and possibly null) check       root = new Entry<>(key, value, null);     size = 1;     modCount++;     return null; }

    

   2.当树根存在直接按照排序查找到指定的节点（左孩子必然小于本身 右孩子必然大于本身 不支持相同大小，也就是当大小相同直接替换并返回old value）

int cmp; Entry<K,V> parent; // split comparator and comparable paths Comparator<? super K> cpr = comparator; if (cpr != null) {     do {         parent = t;         cmp = cpr.compare(key, t.key);         if (cmp < 0)             t = t.left;         else if (cmp > 0)             t = t.right;         else             return t.setValue(value);     } while (t != null); } else {     if (key == null)         throw new NullPointerException();     Comparable<? super K> k = (Comparable<? super K>) key;     do {         parent = t;         cmp = k.compareTo(t.key);         if (cmp < 0)             t = t.left;         else if (cmp > 0)             t = t.right;         else             return t.setValue(value);     } while (t != null); } Entry<K,V> e = new Entry<>(key, value, parent); if (cmp < 0)     parent.left = e; else     parent.right = e;

3. 如果这是一根平衡二叉树那么由于数据的插入很可能导致失衡，那么可能需要一系列的旋转来完成二叉树的平衡（平衡的目的在于更好的查找速度）
大学里面可能都学过AVL树其实就是一种典型的平衡二叉树的实现（但是avl的旋转次数可能较多，导致整体统计性能不如红黑树）

在插入新的节点之后首先要做的就是重新平衡（旋转或者着色） 

fixAfterInsertion(e);

/** From CLR */ private void rotateLeft(Entry<K,V> p) {     if (p != null) {         Entry<K,V> r = p.right;         p.right = r.left;         if (r.left != null)             r.left.parent = p;         r.parent = p.parent;         if (p.parent == null)             root = r;         else if (p.parent.left == p)             p.parent.left = r;         else             p.parent.right = r;         r.left = p;         p.parent = r;     } }   /** From CLR */ private void rotateRight(Entry<K,V> p) {     if (p != null) {         Entry<K,V> l = p.left;         p.left = l.right;         if (l.right != null) l.right.parent = p;         l.parent = p.parent;         if (p.parent == null)             root = l;         else if (p.parent.right == p)             p.parent.right = l;         else p.parent.left = l;         l.right = p;         p.parent = l;     } }   /** From CLR */ private void fixAfterInsertion(Entry<K,V> x) {     x.color = RED;       while (x != null && x != root && x.parent.color == RED) {         if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {             Entry<K,V> y = rightOf(parentOf(parentOf(x)));             if (colorOf(y) == RED) {                 setColor(parentOf(x), BLACK);                 setColor(y, BLACK);                 setColor(parentOf(parentOf(x)), RED);                 x = parentOf(parentOf(x));             } else {                 if (x == rightOf(parentOf(x))) {                     x = parentOf(x);                     rotateLeft(x);                 }                 setColor(parentOf(x), BLACK);                 setColor(parentOf(parentOf(x)), RED);                 rotateRight(parentOf(parentOf(x)));             }         } else {             Entry<K,V> y = leftOf(parentOf(parentOf(x)));             if (colorOf(y) == RED) {                 setColor(parentOf(x), BLACK);                 setColor(y, BLACK);                 setColor(parentOf(parentOf(x)), RED);                 x = parentOf(parentOf(x));             } else {                 if (x == leftOf(parentOf(x))) {                     x = parentOf(x);                     rotateRight(x);                 }                 setColor(parentOf(x), BLACK);                 setColor(parentOf(parentOf(x)), RED);                 rotateLeft(parentOf(parentOf(x)));             }         }     }     root.color = BLACK; }

这边首先描述一下红黑树的定义

除了二叉树的基本要求外，红黑树必须满足以下几点性质。

1. 节点必须是红色或者黑色。
2. 根节点必须是黑色。
3. 叶节点(NIL)是黑色的。（NIL节点无数据，是空节点）
4. 红色节点必须有两个黑色儿子节点。
5. 从任一节点出发到其每个叶子节点的路径，黑色节点的数量是相等的。

先查看一下节点的定义

/**  * Node in the Tree.  Doubles as a means to pass key-value pairs back to  * user (see Map.Entry).  */   static final class Entry<K,V> implements Map.Entry<K,V> {     K key;     V value;     Entry<K,V> left = null;     Entry<K,V> right = null;     Entry<K,V> parent;     boolean color = BLACK;       /**      * Make a new cell with given key, value, and parent, and with      * {@code null} child links, and BLACK color.      */     Entry(K key, V value, Entry<K,V> parent) {         this.key = key;         this.value = value;         this.parent = parent;     }       /**      * Returns the key.      *      * @return the key      */     public K getKey() {         return key;     }       /**      * Returns the value associated with the key.      *      * @return the value associated with the key      */     public V getValue() {         return value;     }       /**      * Replaces the value currently associated with the key with the given      * value.      *      * @return the value associated with the key before this method was      *         called      */     public V setValue(V value) {         V oldValue = this.value;         this.value = value;         return oldValue;     }       public boolean equals(Object o) {         if (!(o instanceof Map.Entry))             return false;         Map.Entry<?,?> e = (Map.Entry<?,?>)o;           return valEquals(key,e.getKey()) && valEquals(value,e.getValue());     }       public int hashCode() {         int keyHash = (key==null ? 0 : key.hashCode());         int valueHash = (value==null ? 0 : value.hashCode());         return keyHash ^ valueHash;     }       public String toString() {         return key + "=" + value;     } }

左旋操作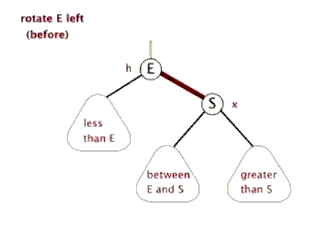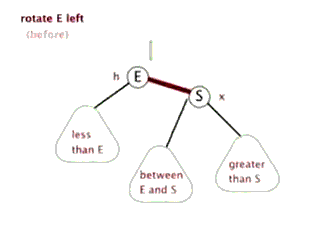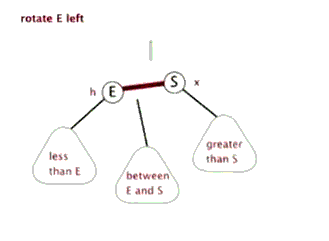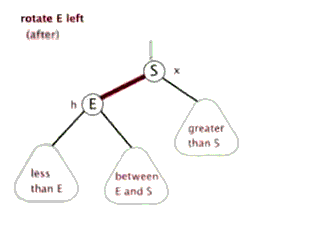

右旋操作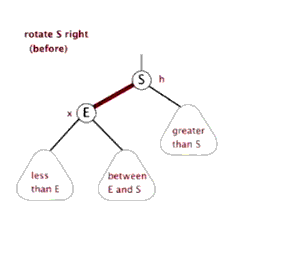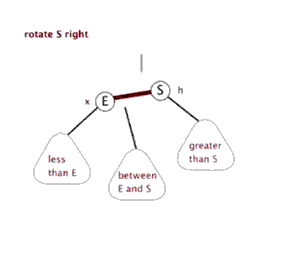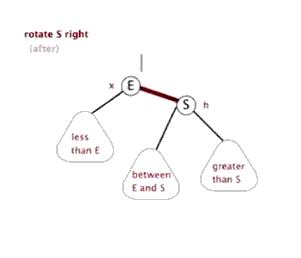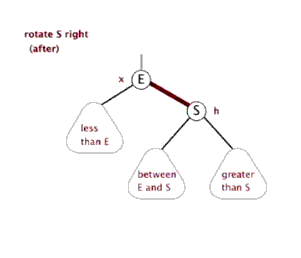

那么分几个场景来讨论插入：【默认孩子节点都是红色，设想如果颜色为黑色那么破坏了第五条特性，那么造成的旋转次数可能较多，实现相对困难】

1. 当父亲节点是黑色，那么无需操作，直接插入新的红色孩子节点（不会破坏属性）
2. 当父亲节点为红色（此时必然会破坏第4条特性）【以下操作均需要注意叔叔节点或者祖父节点均有可能不存在】===》当然此时祖父节点必然存在因为根节点必须为黑色
   以父亲为左孩子为例，其余镜像即可
   1. 当叔叔节点为红色，此时将父亲节点和叔叔节点涂成黑色，同时将祖父节点涂成红色，并将当前指针指向祖父节点
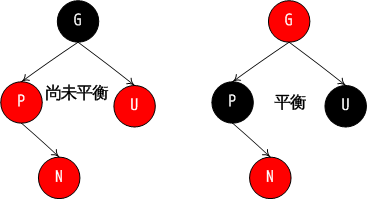
   2. 当叔叔节点为黑色，当前节点为父亲节点的右孩子 此时以父亲节点进行左旋 并将当前指针指向原父亲节点
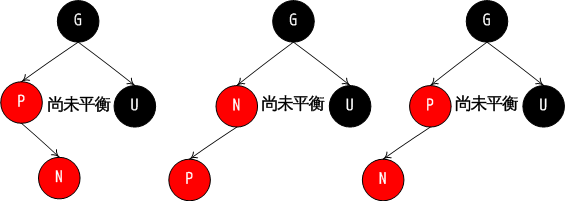
   3. 当叔叔节点为黑色，当前节点为父亲节点左孩子 那么需要以父亲节点右旋 同时将父亲节点涂黑 原祖父节点涂红

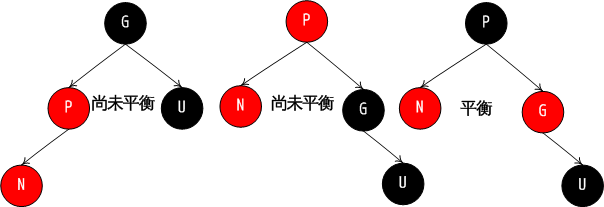
考虑一下左旋或者右旋的情况，事实上为了高度尽可能的低（最好是完美平衡二叉树）那么当新加的节点是左孩子自然要进行右旋（这样高度相应降低）右孩子自然进行左旋【这也是常规思路】 其余分情况进行颜色变更

那么从代码分析

/** From CLR */ private void fixAfterInsertion(Entry<K,V> x) {     x.color = RED;       while (x != null && x != root && x.parent.color == RED) {         if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {             //父亲节点为祖父节点的左孩子节点             Entry<K,V> y = rightOf(parentOf(parentOf(x)));             if (colorOf(y) == RED) {                 //父亲节点和叔叔节点均为红色                 setColor(parentOf(x), BLACK);                 setColor(y, BLACK);                 setColor(parentOf(parentOf(x)), RED);                 x = parentOf(parentOf(x));                 //对应情况A             } else {                  //父亲节点为红色和叔叔节点为黑色                 if (x == rightOf(parentOf(x))) {                    //自身是父亲节点的右孩子 左旋父亲 指针并指向父亲节点                     x = parentOf(x);                     rotateLeft(x);                     //对应情况B                 }                 //此时指针已经变成原父亲节点 逻辑走到情况C 所以此时的叔叔节点并未发生变化 因此叔叔节点仍然为黑色                 setColor(parentOf(x), BLACK);                 setColor(parentOf(parentOf(x)), RED);                 rotateRight(parentOf(parentOf(x)));                 //父亲涂红色 祖父涂黑色 父亲右旋 对应情况C             }         } else {             //父亲节点为祖父节点的右孩子节点             Entry<K,V> y = leftOf(parentOf(parentOf(x)));             if (colorOf(y) == RED) {                 //父亲节点和叔叔节点均为红色                 setColor(parentOf(x), BLACK);                 setColor(y, BLACK);                 setColor(parentOf(parentOf(x)), RED);                 x = parentOf(parentOf(x));                 //对应情况A             } else {                 if (x == leftOf(parentOf(x))) {             //自身是父亲节点的左孩子 右旋父亲 指针并指向父亲节点                     x = parentOf(x);                     rotateRight(x);             //对应情况B                 }                 setColor(parentOf(x), BLACK);                 setColor(parentOf(parentOf(x)), RED);                 rotateLeft(parentOf(parentOf(x)));                 //父亲涂黑色 祖父涂红色 父亲左旋 对应情况C             }         }     }     root.color = BLACK; //根节点必须为黑色 }

参考 http://www.cnblogs.com/hilow/p/3949188.html

http://blog.csdn.net/chenssy/article/details/26668941

http://www.cnblogs.com/daoluanxiaozi/p/3340382.html

https://zhuanlan.zhihu.com/p/24795143?refer=dreawer

http://www.cnblogs.com/yangecnu/p/Introduce-Red-Black-Tree.html