链表中环的检测是一个超级经典的问题...我以前面试的时候就被问到过，然后...当时场面一度十分尴尬~哈哈哈哈~废话不多说，本篇文章整理一下关于单链表中环的检测的一些问题。

综述

关于链表中环的检测，相关问题一般有如下几种：

1. 给定一个单链表，判断其中是否有环的存在
2. 如果存在环，找出环的入口点
3. 如果存在环，找出环上结点的个数
4. 如果存在环，求出链表的长度
5. 如果存在环，求出环上距离任意一个结点最远的结点（环的对面结点问题）
6. 判断两个无环链表是否相交
7. 如果相交，求出第一个相交结点

针对如上七种问题，下面我们逐一进行分析并写出相应实现代码。

判断是否有环

问题分析

对于这个问题，有一种非常巧妙的“快慢指针”的方法，就是定义两个指针：fast和slow，最初的时候fast和slow都指向链表的初始结点head，然后每一次操作，fast向前走两步，slow向前走一步。
因为fast比slow移动快，如果有环，那么fast一定会先进入环，而slow后进入环。当两个指针都进入环后，经过一定次数的操作，fast和slow最终会在环上相遇，并且一定是在slow绕环走完一圈之前相遇。

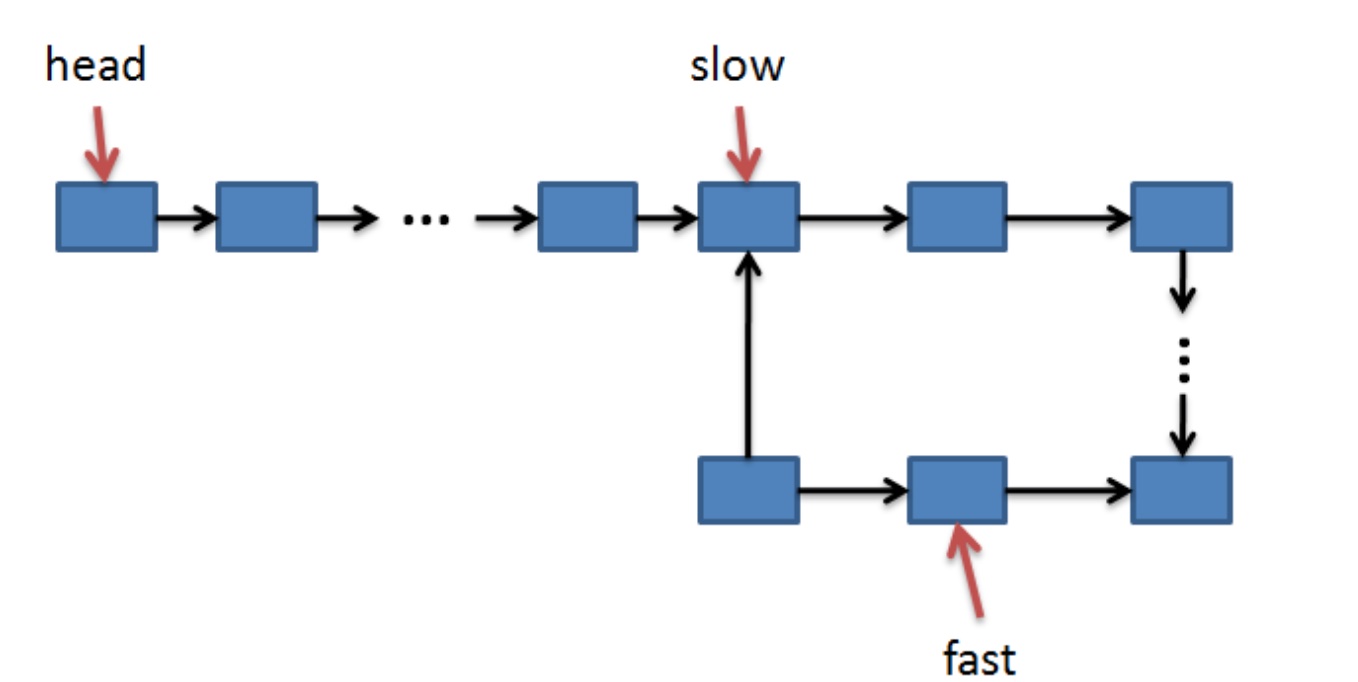
如图所示，slow进入环时，fast可能处于图示状态，然后每次操作，slow会向前走一步，而fast会向前追两步。因此每次操作完fast到slow的距离都会缩短一步，5、4、3、2、1...直到相遇。
又因为同一个环中，slow和fast的距离不可能大于环的总长度，所以fast和slow一定会在slow走完一圈之前相遇。
特殊情况：开始时，slow和fast就在环的入口处，这样相遇时，slow刚好走完一圈。

实现代码

typedef struct node{
    char data;
    node *next;
}Node;
bool exitLoop(Node * head){
    Node *fast , *slow;
    slow = fast = head;
    
    while( fast->next != NULL && slow != NULL)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow==fast) return true;
    }
    return false;
}

找出环的入口点

这个题也比较巧妙，需要先推导一下，最好准备一下纸笔，跟我一块算一下。

问题分析

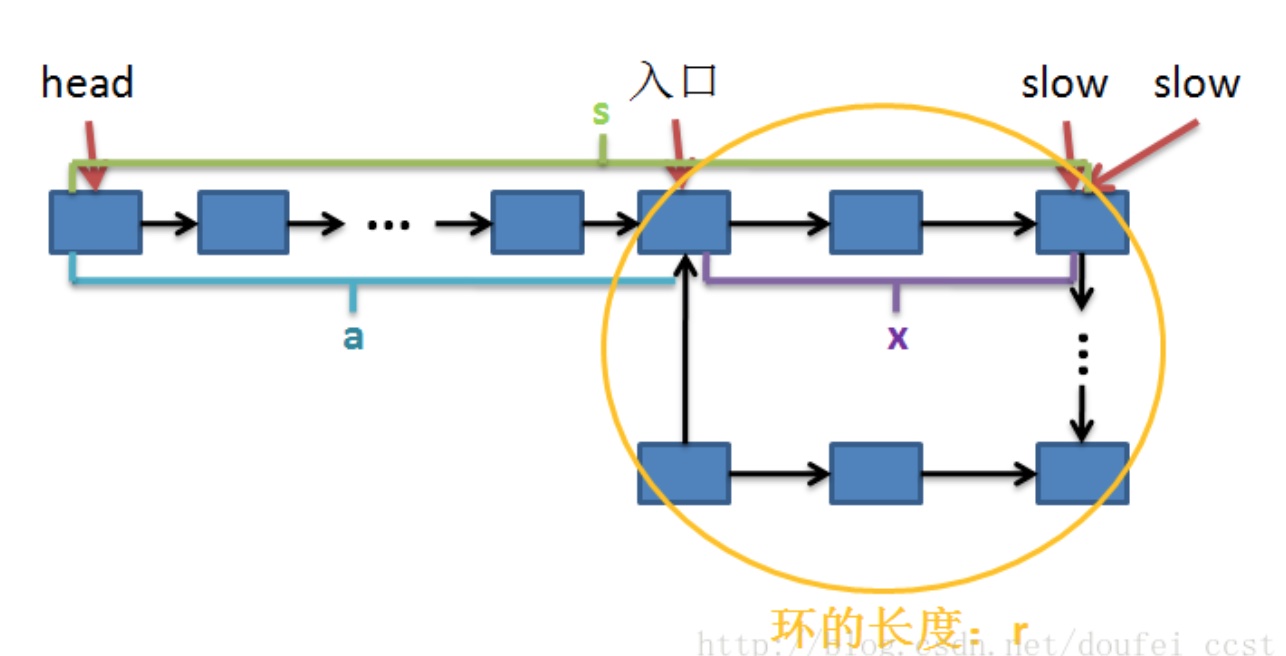
如果链表有环，则在slow绕环走完一圈之前，一定会和fast相遇。
我们假设相遇时slow走了s个结点，则fast走了2s个结点。
设环的长度为r，相遇时fast已绕环走了 n 圈(n>=1)，可得等式：
2s = s + n r 简化得 => s = n r
又设head与环的入口点距离为 a ，入口点与相遇点的距离为 x ，根据slow的总路径为s可得：
s = a + x
结合上式：a + x = n r 变形 => a + x = ( n - 1 ) r + r
设链表总长度为L，则：r = L - a ，带入上式，得：a = ( n - 1 ) * r + ( L - a - x )
好了，注意看图，L - a - x 的长度就是从相遇点到环入口点的长度，也就是说，如果我们放置两个指针p1和p2，分别从起始点和相遇点出发，那么在p2绕环 ( n - 1 ) 圈后，最终一定会在环的入口点和p1相遇。
这样，我们就得到了环的入口点。

代码实现

typedef struct node{
    int elem;
    struct node * next;
}Node, *NodeList;

//寻找环的入口点
NodeList FindLoopPort(NodeList head)
{
    NodeList slow=head,fast=head;
    //得到相遇点
        while( fast->next != NULL && fast != NULL)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow==fast) break;
    }
    if(fast == NULL || fast->next==NULL)
        return NULL;
    //slow指在开头，fast指在相遇点
    //得到入口点
    slow=head;
    while( slow != fast ){
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}

找出环上结点的个数

问题分析

对于这个问题，有两种常见的解决方法：

1. 在slow和fast相遇后，让其中一个继续向前走，下次相遇时，所经过的结点，就是环上的结点个数。
2. 在slow和fast相遇后，让slow和fast同时继续向前走，下次相遇时，所经过的结点，就是环上的结点个数。

稍微解释一下第二种方法，因为slow和fast的速度不同，同时出发后，两指针最大距离为环的总长度r，然后每次操作距离都会缩短一位，最终一定会再次相遇。再次相遇时，正好操作r次，也正好经过r个结点。

方法一实现代码

typedef struct node{
    int elem;
    struct node * next;
}Node, *NodeList;

//寻找环的入口点
NodeList FindLoopPort(NodeList head)
{
    NodeList slow=head,fast=head;
    //得到相遇点
        while( fast->next != NULL && fast != NULL)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow==fast) break;
    }
    if(fast == NULL || fast->next==NULL)
        return NULL;
    //fast停止，slow继续向前走
    //得到再次相遇点
        int count=0;//计数器
    while( slow != fast ){
            count ++;
      slow = slow->next;
    }
    return count;
}

求出链表的长度

问题分析

链表长度L = 起点到入口点的距离 + 环的长度r ;
在前面的基础上，我们可以很轻松的得到这个题目的解。

求出环上距离任意一个结点最远的结点（环的对面结点问题）

问题分析

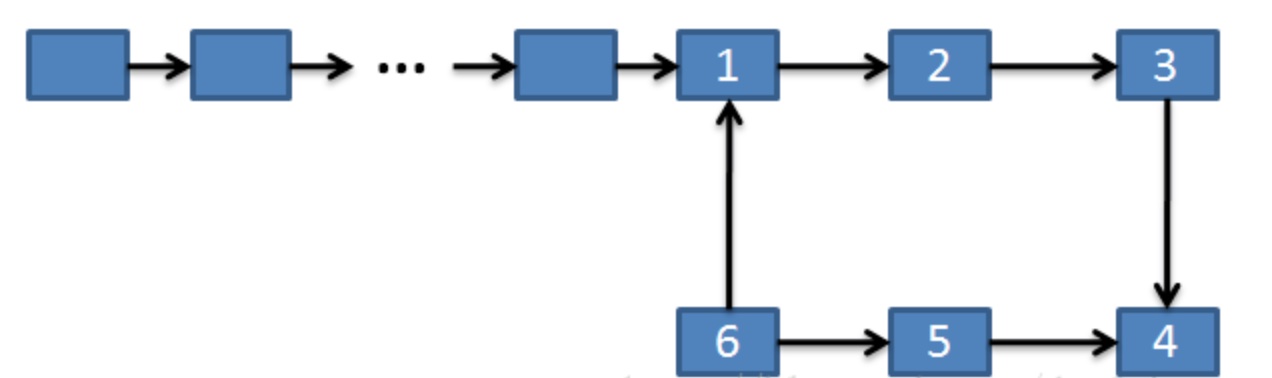
如图所示，结点1和结点4，结点2和结点5，结点3和结点6分别互为“对面结点”，也就是环上距离最远的结点。
我们依然可以使用“快慢指针”的思想来解决这道题，定义一个每次移动两个结点的指针fast和每次移动一个结点的指针slow，两指针同时在问题结点出发，当fast或者fast->next再次回到问题结点时，slow所指向的结点就是问题结点的“对面结点”。

代码实现

typedef struct node{
    int elem;
    struct node * next;
}Node, *NodeList;

//寻找对面结点
NodeList FindFacePort(NodeList prt0)
{
    NodeList slow=prt0,fast=prt0;
        do{
            slow = slow->next;
            fast = fast->next->next;
        } while(fast!=prt0 && fast!=prt0->next);
        return slow;
}

判断两个无环链表是否相交

问题分析

对于判断两个无环链表是否相交类的问题，看起来无从下手，但其实只需要转换一下思路就豁然开朗了。

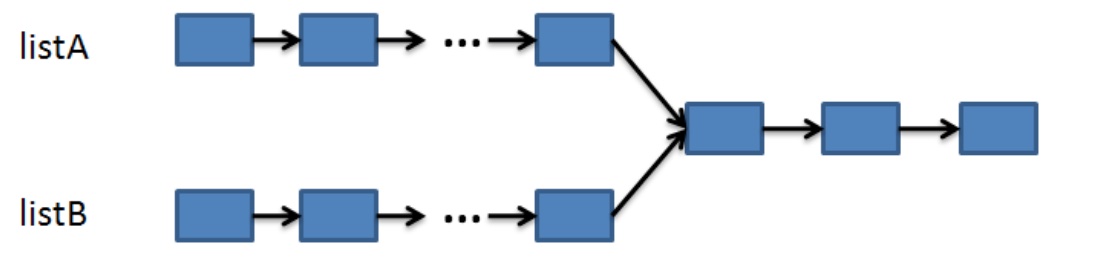
如图所示，存在ListA和ListB两个无环相交链表，我们只需要将ListA的首尾相连，这样就变成我们熟悉的判断是否有环的问题了。
so easy ~

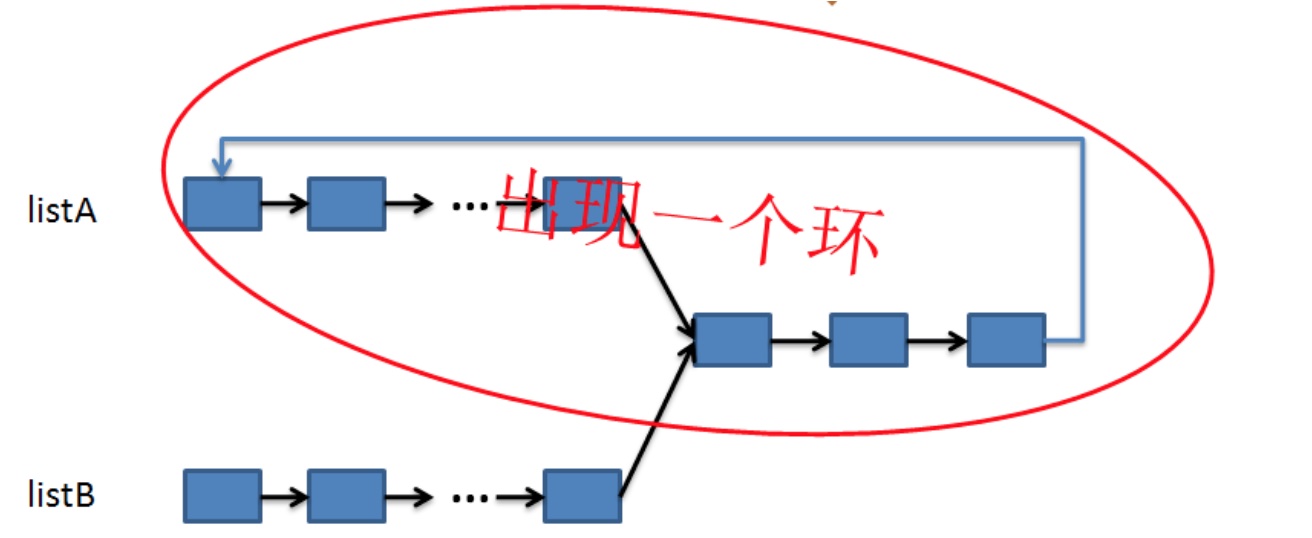
然后是问题七：如果相交，求出第一个相交结点。
同理，可转化为求环的相交点的问题。

参考链接

判断链表中是否有环
求单链表环上节点的数量

最后

关于链表中环的检测，常见的基本就这些了，如果你还有其他想要分享的类型，欢迎留言讨论~