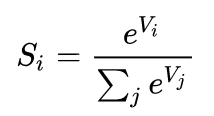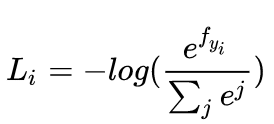在上一次的博客中，我们介绍了如果实现一个最简单的线性回归的模型，今天我们来看一下，如何利用同样的思路实现更多的模型。

逻辑回归

逻辑回归并非只能实现二分类，我们下面就看一个利用逻辑回归（Multinomial logistic regression）实现多分类的例子。

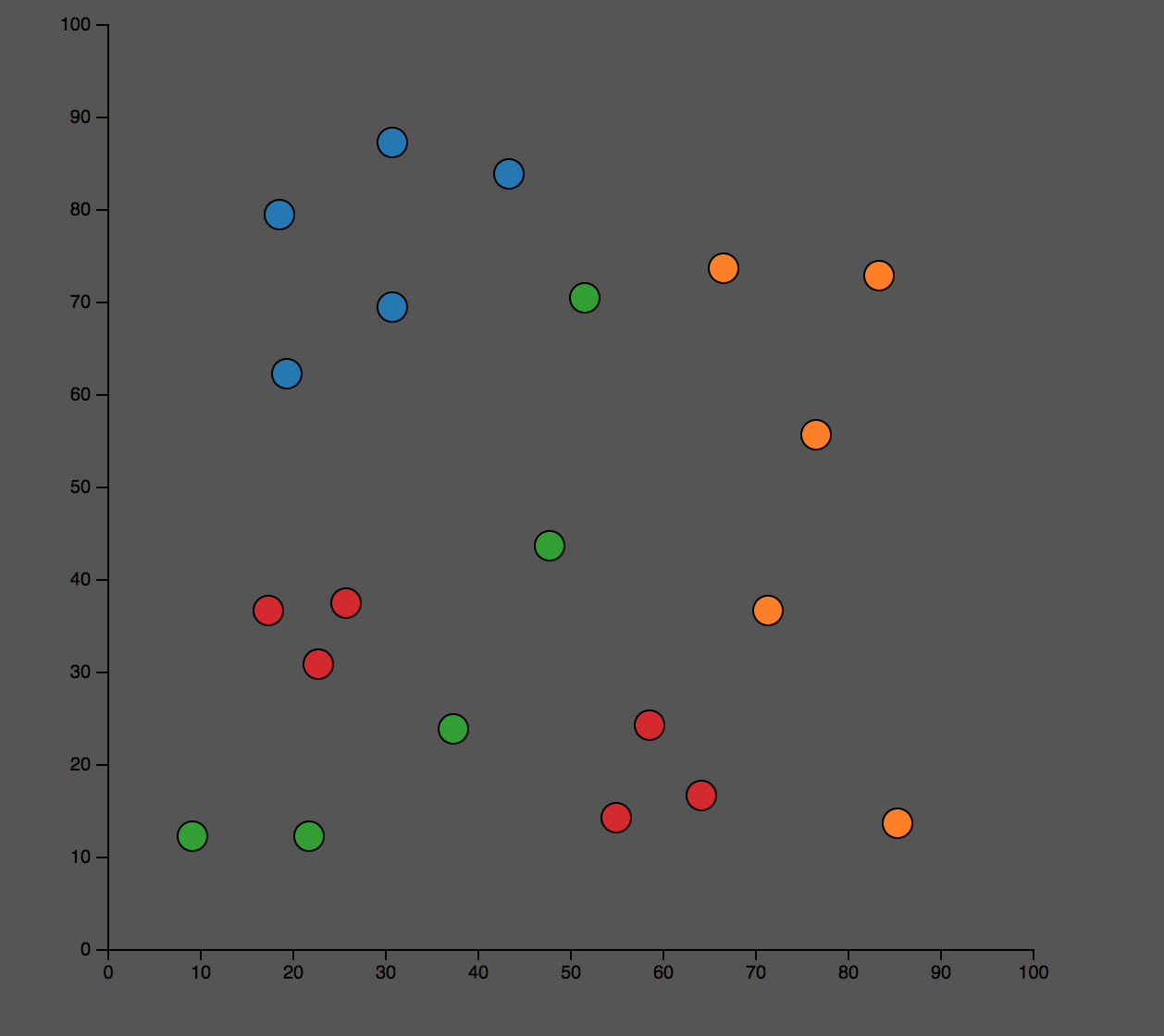
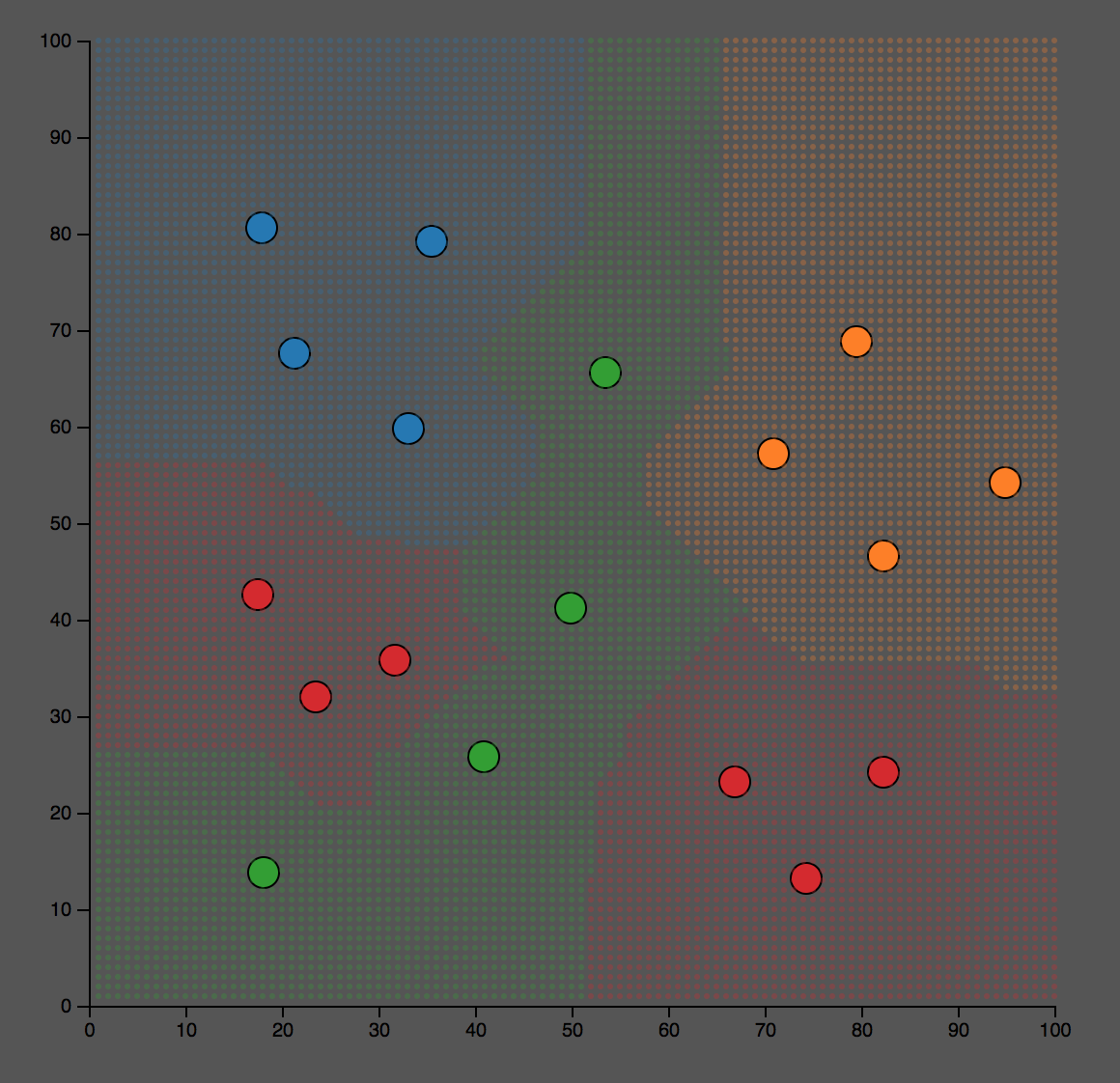
这个是训练数据：

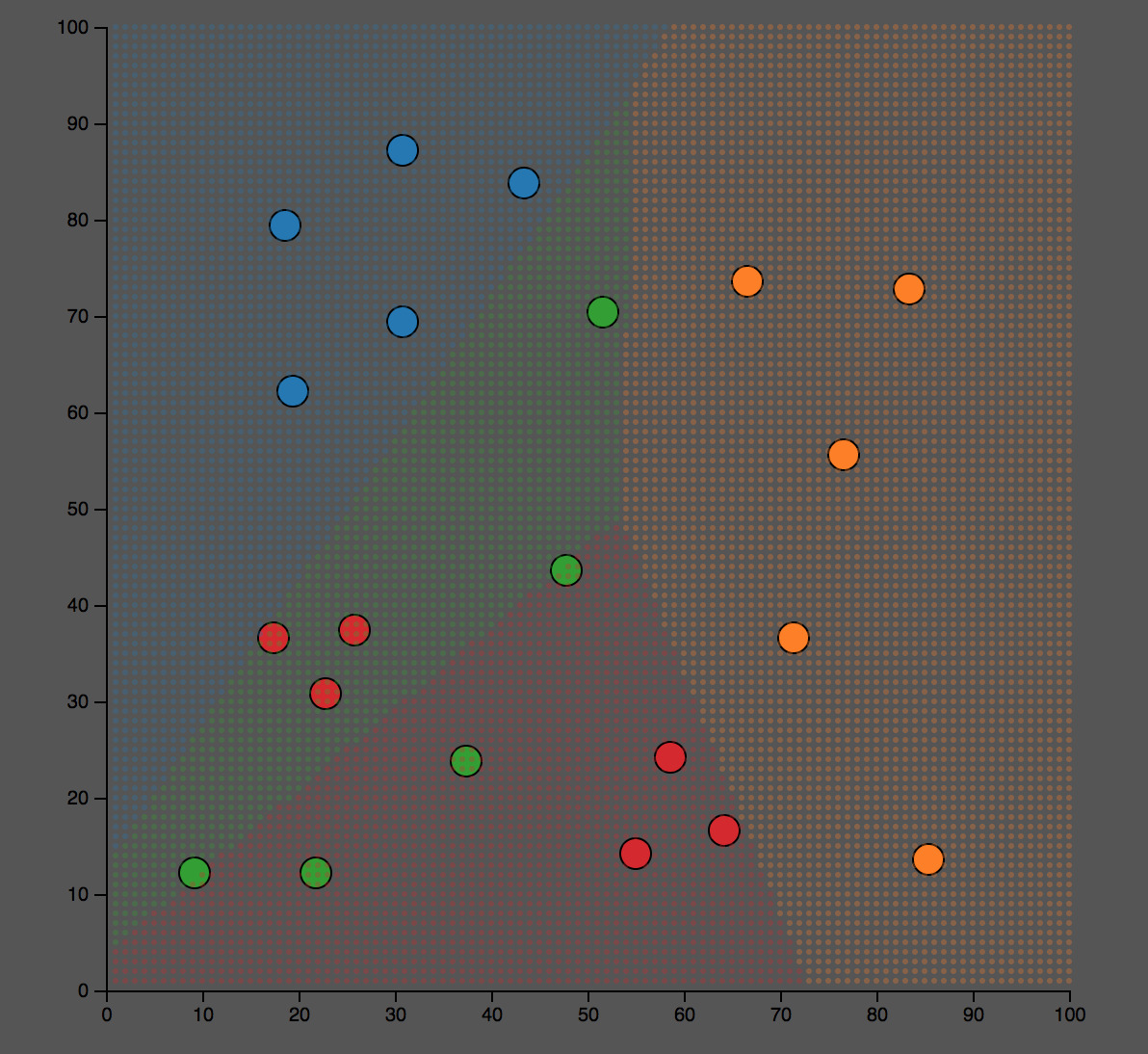
这个是分类的结果。我们可以看到对某些点，蓝色和橙色，分类效果比较好；而对于绿色和红色的点，分类的结果不是很理想。

代码在这里：

function logistic_regression(train_data, train_label) {     const numIterations = 100;   const learningRate = 0.1;   const optimizer = tf.train.adam(learningRate);   //Caculate how many category do we have   const number_of_labels = Array.from(new Set(train_label)).length;   const number_of_data = train_label.length;      const w = tf.variable(tf.zeros([2,number_of_labels]));   const b = tf.variable(tf.zeros([number_of_labels]));      const train_x = tf.tensor2d(train_data);   const train_y = tf.tensor1d(train_label);      function predict(x) {     return tf.softmax(tf.add(tf.matMul(x, w),b));   }   function loss(predictions, labels) {     const y = tf.oneHot(labels,number_of_labels);     const entropy = tf.mean(tf.sub(tf.scalar(1),tf.sum(tf.mul(y, tf.log(predictions)),1)));     return entropy;   }      for (let iter = 0; iter < numIterations; iter++) {     optimizer.minimize(() => {       const loss_var = loss(predict(train_x), train_y);       loss_var.print();       return loss_var;     })       } }

逻辑回归和之前的线性回归的过程基本类似，有几个要注意的地方：

• 训练数据
  • train_x是每一个2维矩阵，每一个点数据就是一个由x,y坐标组成的二元数组 [x,y]
  • train_y是每一点的分类，从0开始
• 预测模型， 对于softmax这个模型，简单说，就是二元逻辑回归向更多元素向量的扩展。有兴趣进一步了解的可以去看下面的这两篇文章：
  
  • 关于softmax和逻辑回归的关系
  • softmax
  • 知乎关于softmax的问答
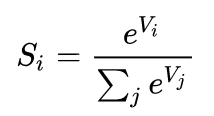
• 损失，损失函数用交叉熵，可以参考这篇文章。
  
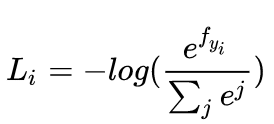
  • 这里在计算损失的时候，对于lable，调用tf.oneHot()方法，把对Label数据变换为以下形式

    // Labels Tensor     [0, 0, 1, 1, 2, 2]  // OneHot Tensor     [[1, 0, 0],      [1, 0, 0],      [0, 1, 0],      [0, 1, 0],      [0, 0, 1],      [0, 0, 1]]

     

K近邻

K近邻是一个特别简单的算法，简单没有训练的过程。大家在我的另一篇关于机器学习的博客里，可以找到对这个算法的可视化介绍。

利用TensorflowJS也可以实现该算法。下面的代码使用L1距离来实现近邻算法（k=1）

function knn(train_data,train_label) {   const train_x = tf.tensor2d(train_data);      return function(x) {     var result = [];     x.map(function(point){       const input_tensor = tf.tensor1d(point);       const distance = tf.sum(tf.abs(tf.sub(input_tensor, train_x)),1);       const index = tf.argMin(distance, 0);       result.push(train_label[index.dataSync()[0]]);     });     return result;   }; }

参考：机器学习下的各种norm到底是个什么东西？

这个算法算然简单，但是计算量不小，预测的效果似乎也不比逻辑回归差呢。我们注意类似的数据和逻辑回归的差异。

某个数学题

同样的，对于一般的学习问题，TensorflowJS自然是不在话下。参考笔者的另一篇博客：一个利用Tensorflow求解几何问题的例子。

代码如下：

function train(train_data) {   const numIterations = 200;   const learningRate = 0.05;   const optimizer = tf.train.sgd(learningRate);      const training_data = tf.tensor2d(train_data);   const center = tf.variable(tf.tensor1d([Math.random()* Math.floor(domain_max),Math.random()* Math.floor(domain_max)]));      // Caculate the distance of this center point to the each point in the training data   const distance = function() {     return tf.pow(tf.sum(tf.pow(tf.sub(training_data, center),tf.scalar(2)),1),tf.scalar(1/2));   }   // Mean Square Error   const loss = function(dis) {     return tf.sum(tf.pow(tf.sub(dis,tf.mean(dis)),tf.scalar(2)));   }   for (let iter = 0; iter < numIterations; iter++) {     var result = {};     optimizer.minimize(() => {       const loss_var = loss(distance());       loss_var.print();       result.loss = loss_var.dataSync();       return loss_var;     })   }   return center; }

运行效果如下：

参考

• 在浏览器中进行深度学习：TensorFlow.js (一）基本概念
• 在浏览器中进行深度学习：TensorFlow.js (二）第一个模型，线性回归
• 一个利用Tensorflow求解几何问题的例子
• 图解机器学习
• Codepen演示代码