背包问题是一个非常典型的问题，围绕他的算法及文章非常多。

实际上本人觉得作为一个程序员，肯定不是碰到一个问题就写一个方式，肯定希望我只要提供简单的几步就搞定我想要的结果，而不是去钻研算法本身。

我把背包问题做了几个抽象：

• 总容量：不管是容积、重量、金钱等等，只要是受限制的，那么就都是一种意义上的总容量

• 单个容量：每个物品的容积、重量、单价等等，都是一种意义上的单个容量

• 装包方式：有01，完全、混合、多重等等各种变种

• 单个价值评估：给出每个物品的价值

至于如果动态规划及价值累计，那就不是使用的人关心的了。

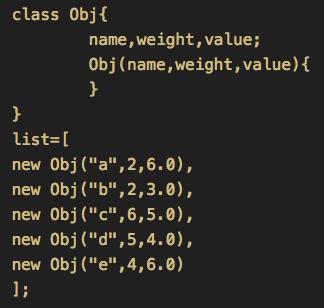
数据准备

上面定义了，一个物品的类，它有name,weight,value三个属性；有一个构造函数，没有函数体表示把参数的值赋给属性；下面建立了一个物品列表。

好的，准备工作就绪，见证奇迹的时刻就要到来了：

• 01背包解法

list=[ new Obj("a",2,6.0), new Obj("b",2,3.0), new Obj("c",6,5.0), new Obj("d",5,4.0), new Obj("e",4,6.0) ]; println("01背包问题:"+list.dpKnapsack(10,list.weight,1,list.value));

上面的含义是：对这个list中的物品进行01背包方式进行获取的最大价值是多少及其获取方法。参数解释：

10：最大重量10

list.weight：物品的重量列表

1：表示每个物品都是最多1个

运行结果：

01背包问题:

[ {result=15.0},  [Obj[name=a,weight=2,value=6.0], Obj[name=b,weight=2,value=3.0], Obj[name=e,weight=4,value=6.0]],  [1, 1, 1] ]

结果解释：

{result=15.0}表示，最后取出来的最大价值

[Obj[name=a,weight=2,value=6.0], Obj[name=b,weight=2,value=3.0], Obj[name=e,weight=4,value=6.0]]表示最后取出来的3个物品。

[1, 1, 1]表示每个物品的取出数量，下标顺序和物品相对应。

• 完全背包解法

list=[ new Obj("a",2,6.0), new Obj("b",2,3.0), new Obj("c",6,5.0), new Obj("d",5,4.0), new Obj("e",4,6.0) ]; println("完全背包问题:"+list.dpKnapsack(10,list.weight,list.value));

上面的含义是：对这个list中的物品进行完全背包方式进行获取的最大价值是多少及其获取方法。参数解释：

10：最大重量10

list.weight：物品的重量列表

list.value：每个物品的价值列表

运行结果：

完全背包问题:

[{result=30.0}, [Obj[name=a,weight=2,value=6.0]], [5]]

结果解释：

{result=30.0}表示，最后取出来的最大价值

[Obj[name=a,weight=2,value=6.0]]表示最后取出来的物品列表。

[5]表示每个物品的取出数量，下标顺序和物品相对应。

• 多重背包

list=[ new Obj("a",12,4.0), new Obj("b",2,2.0), new Obj("c",1,1.0), new Obj("d",4,10.0), new Obj("e",1,2.0) ];  println("多重背包问题:"+list.dpKnapsack(15,list.weight,[1,7,12,3,1],list.value));

上面的含义是：对这个list中的物品进行多重背包方式进行获取的最大价值是多少及其获取方法。参数解释：

15：最大重量15

list.weight：物品的重量列表

[1,7,12,3,1]：表示每个物品对应最多个数

list.value：每个物品对应的价值

运行结果：

多重背包问题:  [ {result=34.0},  [Obj[name=b,weight=2,value=2.0], Obj[name=d,weight=4,value=10.0], Obj[name=e,weight=1,value=2.0]],  [1, 3, 1] ]

结果解释：

{result=34.0}表示，最后取出来的最大价值

[Obj[name=b,weight=2,value=2.0], Obj[name=d,weight=4,value=10.0], Obj[name=e,weight=1,value=2.0]]表示最后取出来的3个物品。

[1, 3, 1]表示每个物品的取出数量，下标顺序和物品相对应。

• 混合背包

list=[ new Obj("a",12,4.0), new Obj("b",2,2.0), new Obj("c",1,1.0), new Obj("d",4,10.0), new Obj("e",1,2.0) ];  println("多重背包问题:"+list.dpKnapsack(15,list.weight,[1,7,12,3,-1],list.value));

上面的含义是：对这个list中的物品进行多重背包方式进行获取的最大价值是多少及其获取方法。参数解释：

15：最大重量15

list.weight：物品的重量列表

[1,7,12,3,-1]：表示每个物品对应最多个数，-1表示不限制次数

list.value：每个物品对应的价值

运行结果：

多重背包问题:  [ {result=36.0},  [Obj[name=d,weight=4,value=10.0], Obj[name=e,weight=1,value=2.0]],  [3, 3] ]

结果解释：

{result=36.0}表示，最后取出来的最大价值

[Obj[name=d,weight=4,value=10.0], Obj[name=e,weight=1,value=2.0]]表示最后取出来的物品列表。

[3, 3]表示每个物品的取出数量，下标顺序和物品相对应。

这次的示例都是典型的背包问题，下次讲带来深入解决实际问题的示例，感兴趣的同学请关注我，以便及时收到推送。

注：此次语言采用本人新作tinyscript，正在进行文档及示例工作，即将正式开源，敬请期待。